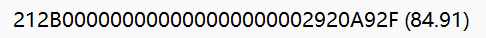IC卡金额算法破解的一次尝试
时隔快一年,终于想起来要更新IC卡算法破解的第二期了。之前第一篇关于水卡密钥算法的破解那篇博客,还是我高三时候写的了,现在大一了,写出的东西也会不一样了。这次会介绍的详细一点了。
第一篇博客传送门:IC卡秘钥算法破解的一次尝试,不过那也只是我高中时候对水卡密钥的理解,现在已经不一样了。OK,现在我来介绍我最近一次,帮别人研究水卡金额的算法的一次尝试,感谢@W提供素材。
警告:本文仅供学习讨论使用,请勿拿去进行其他不法用途,出什么问题,本人概不负责。
0x0.前言
本来没打算写金额篇的,因为高中那会,能力有限,还不能很了解金额算法的一些原理。现在大学了,不在高中,数据也拿不到了,也写不了。但是天无绝人之路,感谢**@W老铁给我提供了数据,让我得以完成水卡算法的第二个部分——金额篇**
0x1.数据准备
这次的数据,可以说是非常的详细,而且数据量也很大。据不完全统计,足足有78条金额数据!!!这么大的数据量,给我的破解提供了很大的便利。
0x2.开始破解算法
拿到数据后,大概了解了一下数据的分布的格式,发现其格式是非常有规律的,如下:
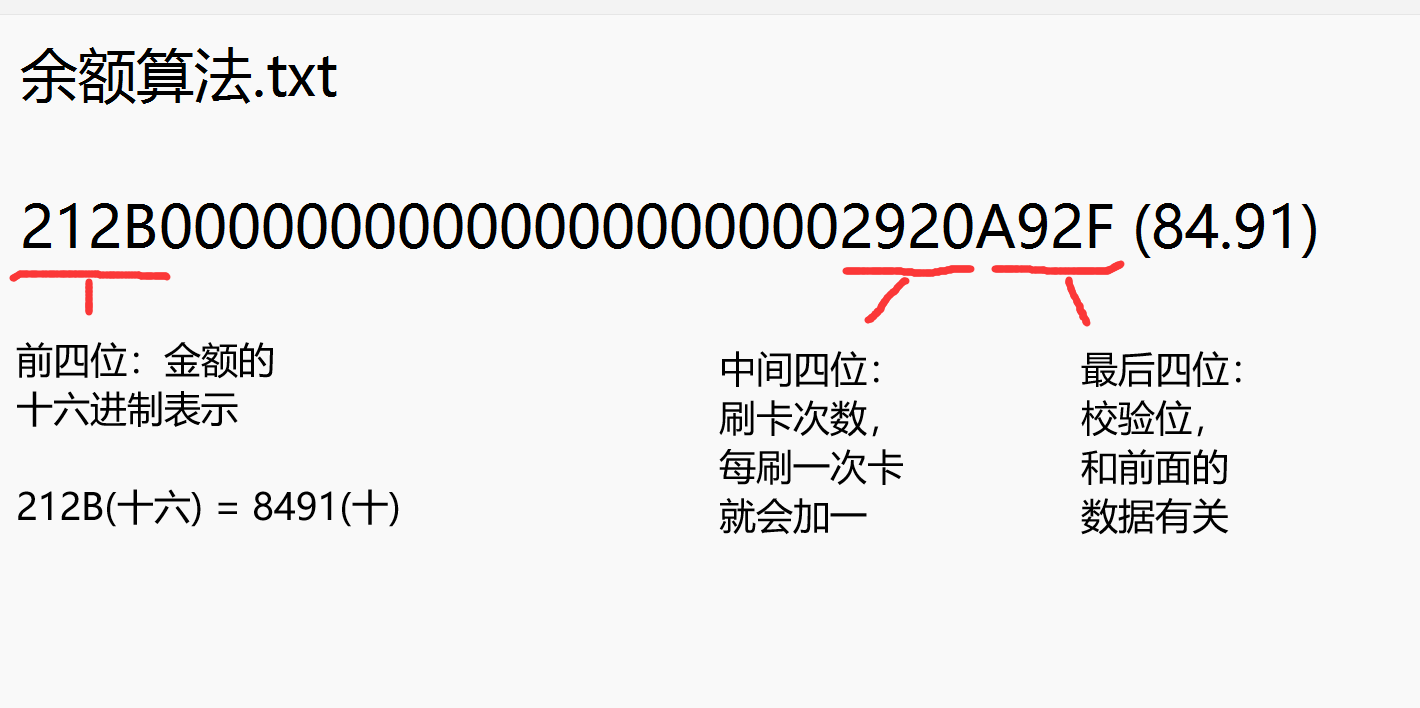
- 前面四位是存储金额的地方,理论最大值是FFFF,也就是655.35元。
- 中间四位是刷卡次数
- 后面四位是校验位,也就是本次破解算法的重点
知道了要破解的数据后,就到了分析数据的环节,这时候就需要大量的数据了:
密密麻麻的数据(晕),这次的数据比较规整,这很利于我们进行数据分析。还记得当时,上C艹课的时候,太无聊了,就在研究这个数据,当时的我还是抱着之前密钥算法破解的思维来尝试破解这个金额算法,这个思维有好处,也有坏处。好处就是我很容易就知道从哪里入手分析,坏处就是,看问题不够全面。不过这些都是正常问题啦。OK,回到主题。
我一开始发现的是后四位的第二位和第四位数字的和,是一个定值——8,例如:
9147 :1 + 7 = 8
894F:9 + F = 24 mod 16 = 8
6E6A:E + A = 24 mod 16 = 8
可以看到,第二位和第四位的值之和都是八(24去求余之后就是8),这样,我们只要知道了第二位的算法,第四位也就可以算出来了。四舍五入,就相当于我们已经搞定了一位的算法了(虽然还不知道第二位怎么得出来的)。这次开局很容易,我就知道了第四位算法,但是接下来得破解工作,就没有这么容易了。
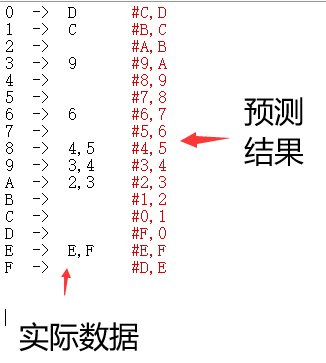
现在还有三位需要破解,因为第四位是由第二位决定的,所以我猜测第三位可能是由第一位决定的(现在看来不完全对)。在前面的48条数据中,可以看到后四位是当金额变化了四次,才变化一次,
而且很多重复出现的。然后我开始找第一位和第三位的对应关系,然后真的找出了一张映射表,
看着这熟悉的变化规律,仿佛之前在密钥算法破解里面见过类似的算法,只要找到什么东西决定第三位是否用进位,然后再找出什么决定第一位,就可以破解出算法了。然而,这个传统的思路虽然看起来很直观,但是,太繁琐了,我隐隐感觉水卡真正的密钥算法应该是非常简洁明了的,破解工作又暂时陷入了僵局。
0x3.突破瓶颈
破解的转折点源自于开始破解工作开始的第二天晚上,那是一个星期五(不是野人),我去参加了社团的系统维护课,课上,讲解了一些数据校验码的知识。其中,用到了许多异或操作,使得运算出来的结果非常有规律。我突然想到,水卡金额校验位是不是也是通过异或得到的呢?有了思路之后,马上开始着手研究,在尝试了许多组合后,终于让我找到了金额校验位计算的真正规律:
后四位校验位是由前面的金额+刷卡次数异或得来的,具体过程是:
以84.91这条数据为例,金额为212B,刷卡次数为2920,校验位为A92F
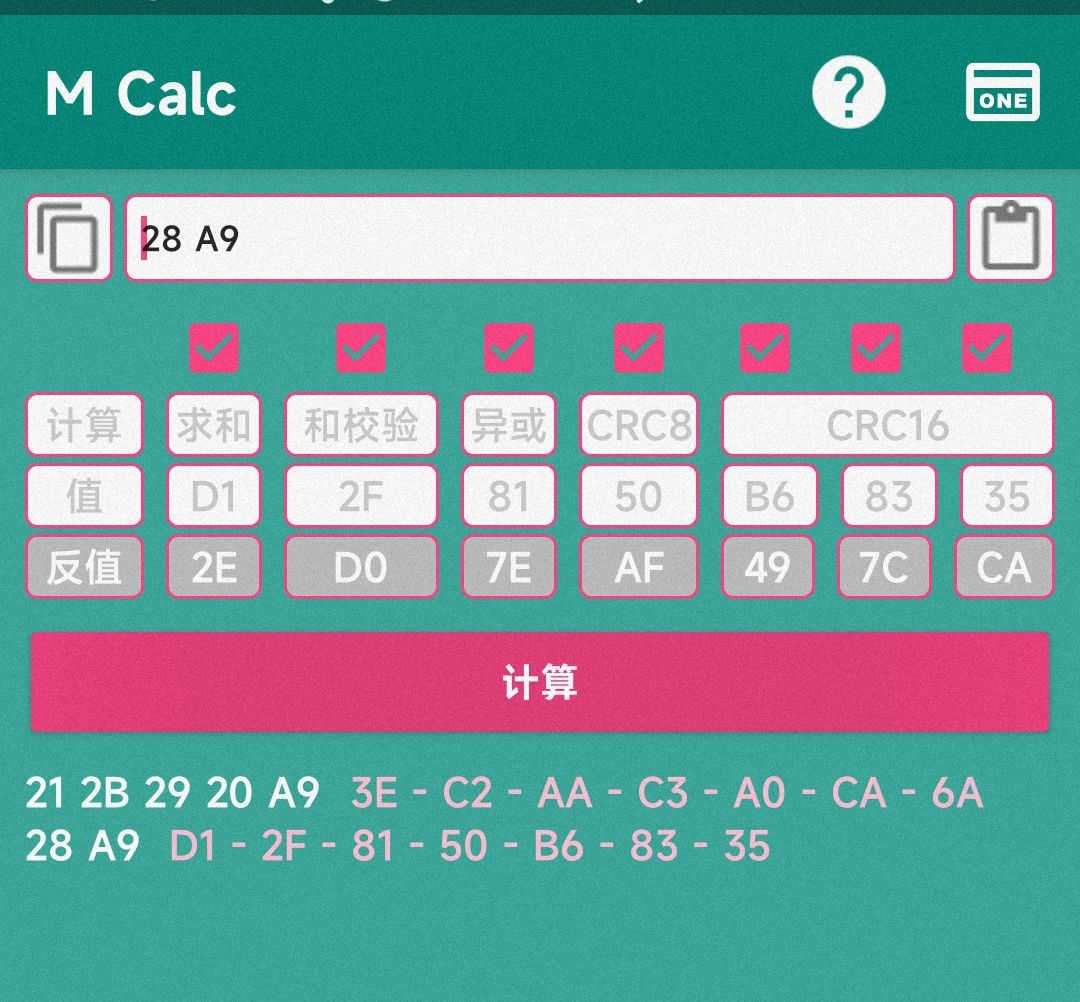
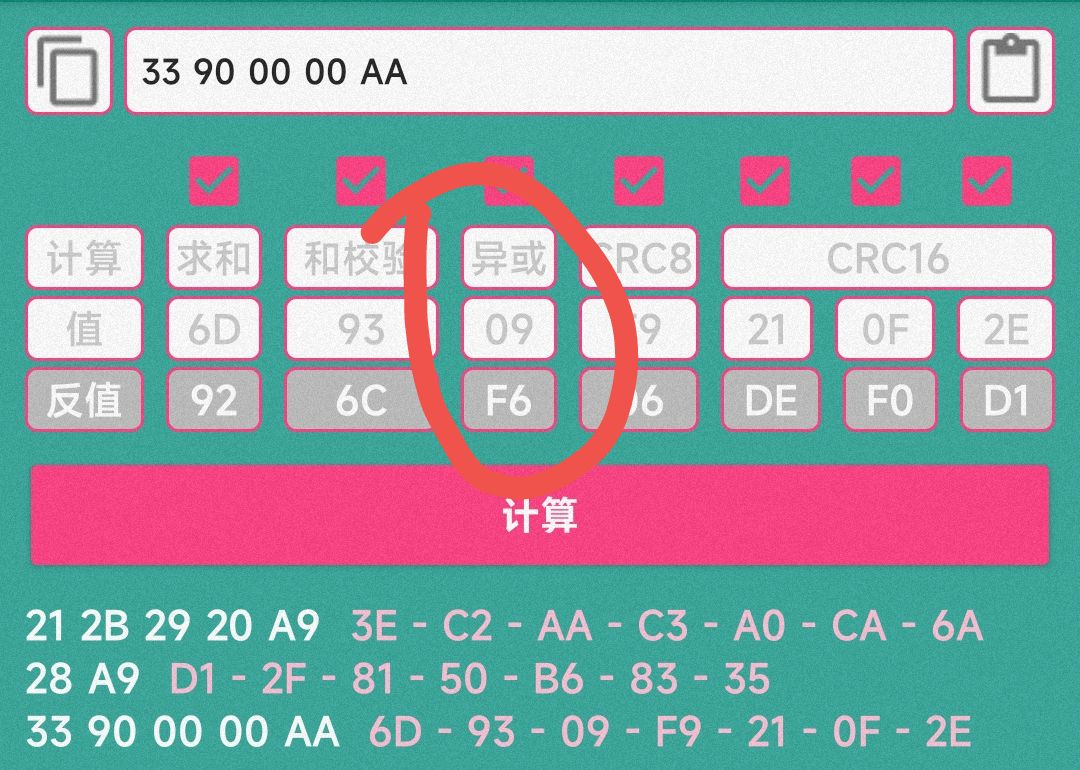
首先,将金额和刷卡次数和校验位前两位进行异或:
21^2B^29^20^A9
= AA
可以看到,结果是AA,再对剩余的数据进行相同的操作可以发现,异或的结果都是AA,所以这就破解出来了校验位的前两位。
然后,经过观察和尝试不难发现,校验位前两位和后两位的和恒为28,所以用A9 与 28进行和校验,可以得出后两位的值
至此,整个金额校验位的算法就破解完毕了,接下来要做的就是实践一下。
0x4.金额模拟
按照上面的方法,我们来随便模拟一个金额写入,比如132.00元,首先13200转换16进制为0x3390
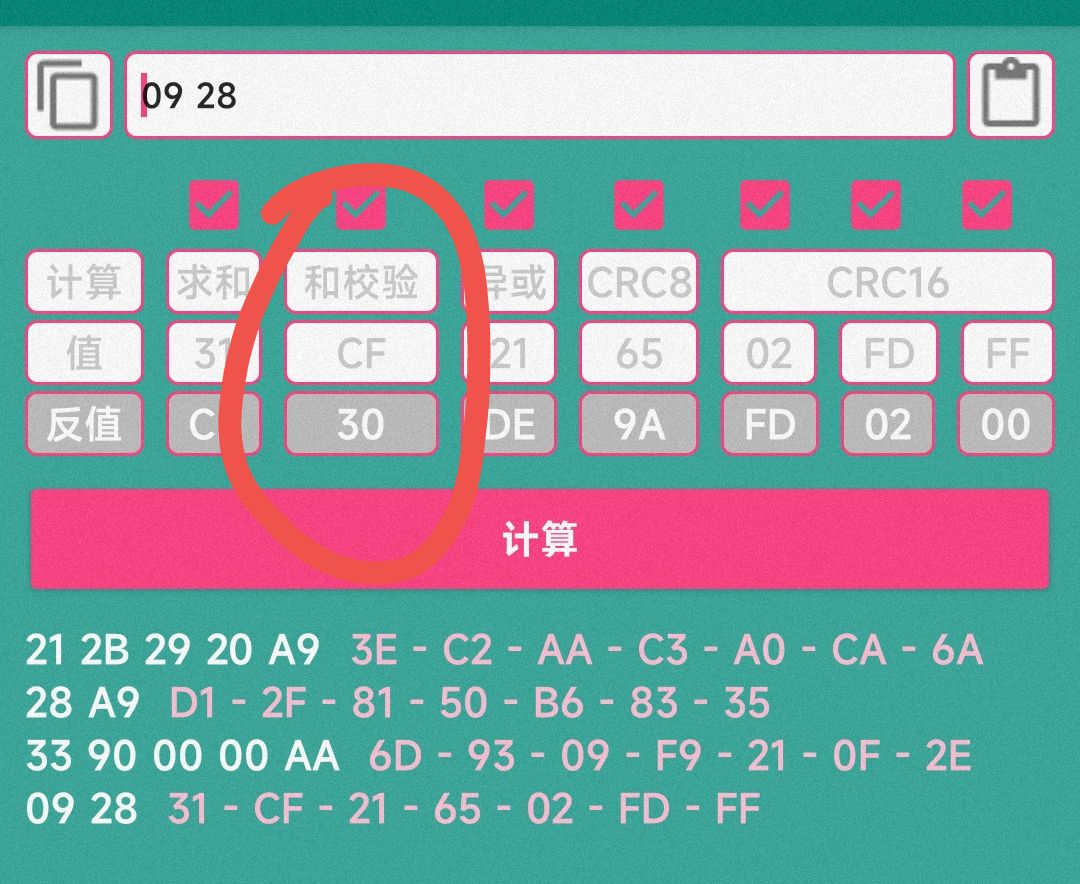
然后,刷卡次数我们可以随便设置,这里我就设置成0000吧。这时候,按照上面的方法,用金额^刷卡次数^AA,就可以得到校验位的前俩位:
前两位是09,再用09与28进行和校验,可以得到
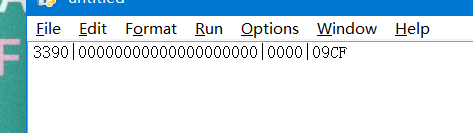
后俩位是CF,所以校验位就是09CF,构造一下金额数据
然后写入卡中去测试一下
可以看到,模拟金额成功了,说明这个算法是正确的呢
0x5.总结
和之前的密钥破解比起来,这次的金额校验位算法破解似乎更简单了,因为现在的我和当初的我不一样了,有那么一点点进步了,所以写这篇文章记录一下。我发现,对于这些M1卡,似乎最常用到的就是异或操作,如果实在没思路,随便尝试异或几个数也是不错的选择呢。